KMP算法，是一种高效的字符串匹配算法。

其主要作用就是在 字符串中 查找子串

BF-暴力匹配算法

找了好几篇文章，都有提到暴力匹配，想必也是绝大部分人遇到字符串匹配时脑海里最快蹦出的思路。

暴力匹配(Brute-Force, BF)算法，正如其名，它的原理非常的简单粗暴。

假定有个字符串 "llligoogle"，我们要判断字符串中是否包含子串 "le" .

暴力匹配：说白了就是子串中的字符，逐一向主串进行匹配。

具体实现:

• 我们通过两个指针 i、j 分别遍历 主串s 和 子串t

• 对比 s[i] 是否等于 t[j]

• 若相等，指针 i、j提示向后移一位，若不相等，j回到子串起始位置，i回到子串遍历次数+1的位置

• 若遍历完整个子串都相等，那就代表主串包含子串

看不懂？没事，上大白话！

拿出刚刚的主串"llligoogle" ，判断是否包含子串 "le"

• le和前面ll比较，第一个l对上，第二个e没对上

• 再和主串的第二个和第三个l比较，也是一样，第一个l对上，第二个e没对上

• 一直到后面，和主串末尾的le匹配上，得出结论，"llligoogle" 包含 "le"

e..就像这样:

怎么有奇奇怪怪的声音，是谁在外放！

一个个字符的去匹配，很明显啊，有种最坏的情况，也就是子串的每个字符要和主串的每个字符都要匹配过去，也就是时间复杂度会来到O(m*n)

我们来看个正经的原理图

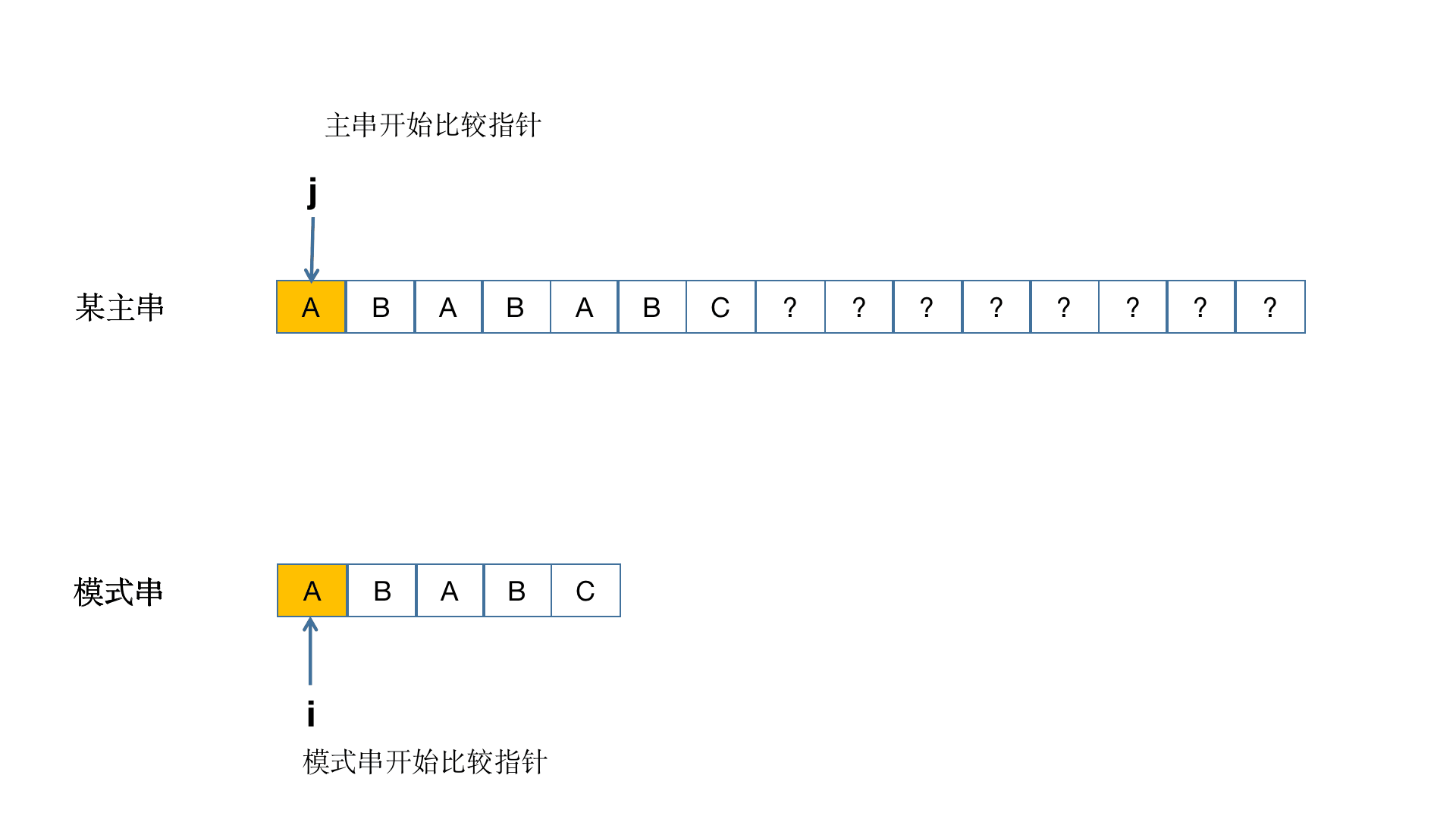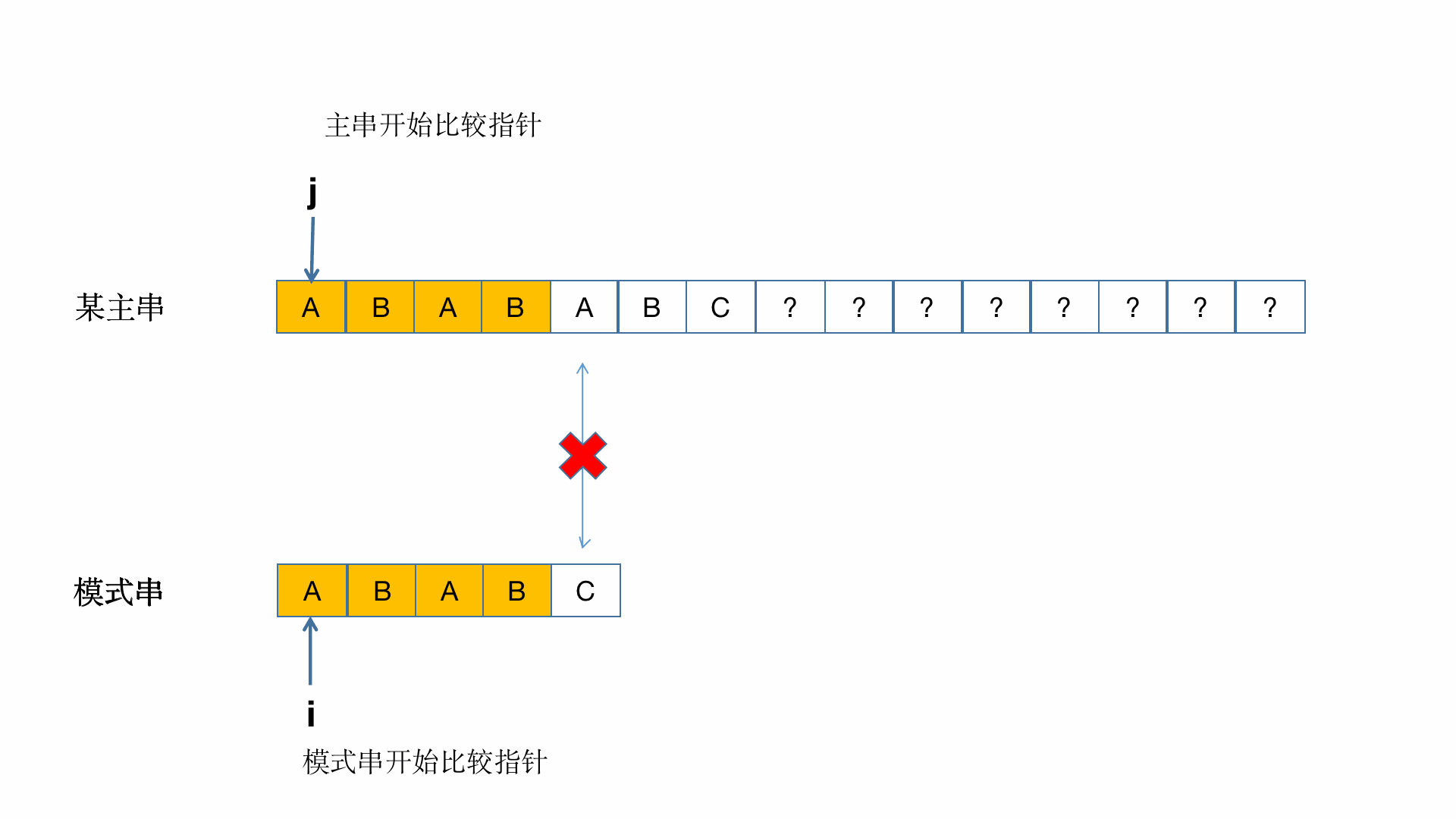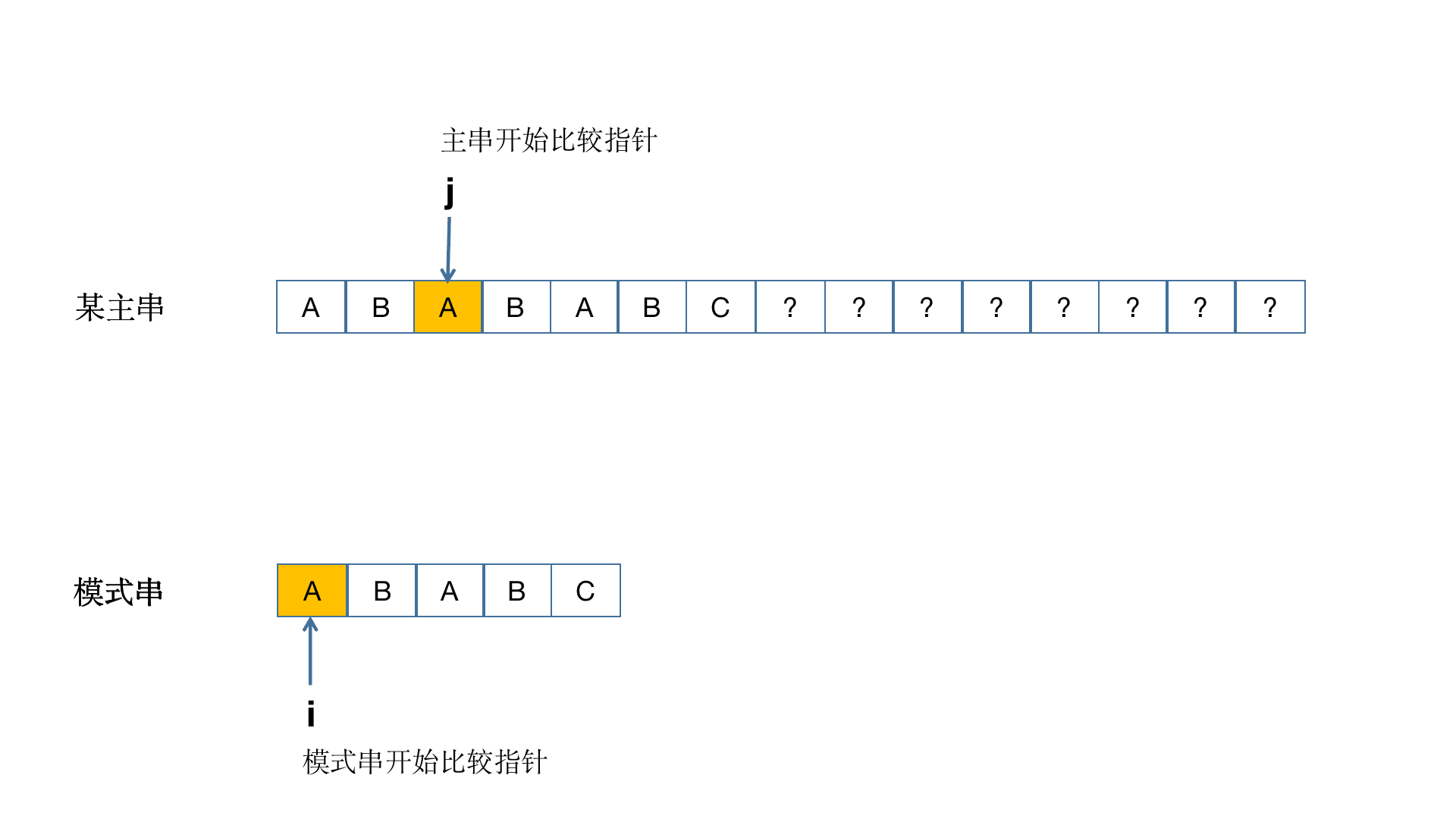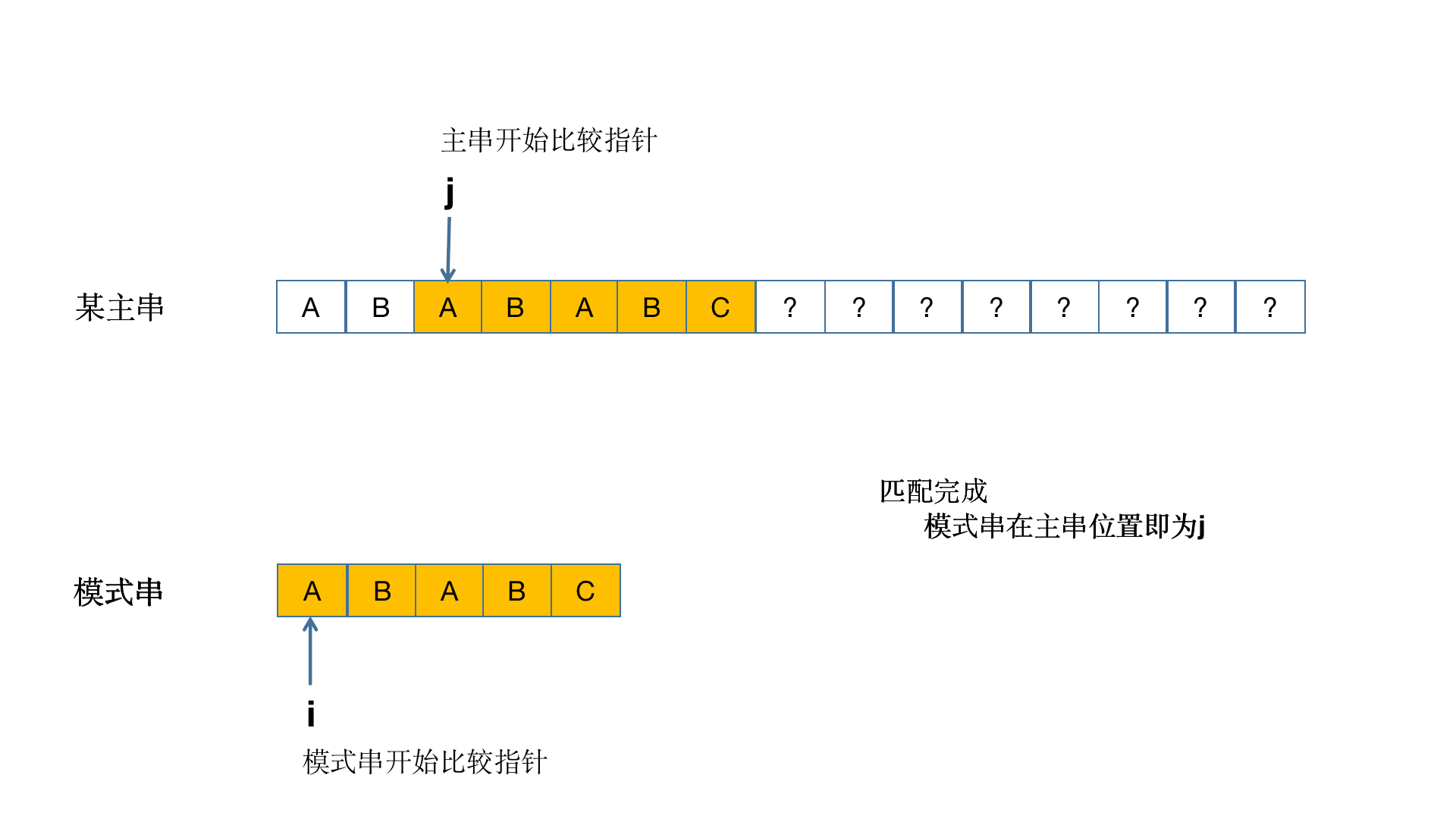
（图片来源:https://blog.csdn.net/weixin_41347419/article/details/114809346）

KMP算法

众所周知，有人问你含暴力二字的算法时，可能它并不是最优解。

BF虽然易于实现，但有个显著的问题，效率慢啊，要是在一本《三国演义》中找出现了几次“俺也一样”，这就很痛苦了。

也没有更好的算法，有，这就是本文接下来介绍的KMP算法。

KMP算法的主要优势就是，只需要一次遍历，就可以找到是否包含子串，也就是说，它的时间复杂度为 O(m+n) 。

其核心思想是，当我们发现一个字符不匹配时，能不能基于已经匹配过的字符，避免指针j回溯，也就是说，指针j永远在主串中 只向前移动。

不算冷的冷知识: KMP算法的名称由它的发明者们的名字首字母组成

分别是: Donald Knuth、James H. Morris 和 Vaughan Pratt 这三位大佬

接下来我们先换个正常点的主串"ABABABCAA" 和子串"ABABC"

next数组

在正式匹配之前，我们要先生成一个next数组

数组中存储了 子串中 每个位置 之前 的 最长 公共前后缀 的 长度

这个长度 也就是匹配失败的时候，下次匹配时 跳过 子串字符 的 数量

让我们先来计算这个长度吧：

首先我们从头到尾先遍历一遍子串，判断遍历到某个字符时，记录遍历过的字符中公共部分的长度

开始匹配

我们已经拿到了next表，就可以开始匹配主串了。

与BF类似，但当我们遇到不匹配的字符时，这次不用回溯指针j，让它停留在原地

然后跳过子串前面的某些字符，继续匹配就行

例如:

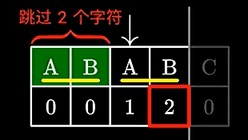
A B A B A B C A A

A B A B C

我们看到，子串最后一个C不匹配

这时候我们看next数组C前一个元素的长度，为2，那下一次遍历时，跳过子串前2个字符

（图片来源:https://www.bilibili.com/video/BV1AY4y157yL/）

也就是:

A B A B A B C A A

- - A B A B C

遍历完子串，没有不匹配的字符，证明主串包含子串

回顾

最后总结以下KMP算法:

KMP算法是一种高效的字符串匹配算法，它通过利用已匹配的字符信息来避免不必要的比较，从而提高了匹配的效率。

KMP算法的核心就是next数组，数组的计算方式如下:

• 初始化Next[0] = 0。

• 对于子串中的每个位置i（从1开始），找到满足P[0...k-1] == P[i-k...i-1]的最长k值，也就是最长前后缀的长度。

• 如果找不到这样的k值，则Next[i] = 0，也就是找不到公共前后缀。

然后就是利用next表进行匹配， 步骤如下:

• 初始化两个指针i和j，分别指向主串和子串的起始位置。 比较S[i]和P[j]，其中S是主串，P是模式串。

• 如果S[i] = P[j]，则i和j都向后移动一位。 如果j = 0（即模式串的第一个字符就不匹配），则i向后移动一位。

• 如果S[i] != P[j]，则j移动到Next[j-1]的位置

• 重复步骤2，直到j等于模式串的长度，表示找到了匹配；或者i等于主串的长度，表示没有找到匹配。

最后放一张原理图:

（图片来源:https://blog.csdn.net/weixin_41347419/article/details/114809346）

其实文章说明还是很晦涩，加上我的表达能力其实一般。

要是还是看不懂的话，建议看看我参考资料第一个链接的视频，描述的要比我的清晰不少。

参考资料:

https://www.bilibili.com/video/BV1AY4y157yL/https://blog.csdn.net/weixin_41347419/article/details/114809346